

Modeling Cryptoeconomic Protocols as Complex Systems - Part 1
In my , we explored the design of The Graph Network in-depth and touched on several focus areas for future research. One of these areas was modeling and simulation, a process we consider essential to correctly parameterizing and hardening the assumptions in our protocol. In this two-part series, we explore the challenges with modeling cryptoeconomic protocols using traditional economic approaches with closed-form solutions and discuss how to leverage tools from engineering and social sciences to aid in the design of a complex protocol.
We’re also excited to announce that we’ll be working with the team to model and simulate The Graph.
Cryptoeconomic Design
Let’s begin by reviewing what we mean when we refer to cryptoeconomic design.
In designing cryptoeconomic systems, we apply theory and mechanisms from economics alongside many of the tools and concepts from computer science that enable cryptocurrency, such as distributed systems and cryptography.
Our goal is to design self-organizing systems, comprising networks of interacting human and autonomous agents, that sustainably optimize for one or more objective functions.
The objective function is the raison d’etre for a protocol or application, and it can be virtually anything. In , for example, the objective function being maximized is presumably the amount of charitable giving on the platform. For , the goal is to provide a high-quality service—indexing and querying decentralized data in the case of The Graph—to any consumer who is willing to pay for it, at the lowest possible price.
A cryptoeconomic protocol comprises incentives, rules, and interfaces.
The agents in these systems self-organize in response to incentives, which are chosen to motivate the behaviors needed for the protocol to function. These behaviors, in turn, are constrained by the rules and interfaces of the protocol.
Vitalik Buterin, who coined the term “cryptoeconomics,” that an important limitation is that we may only set rules that are expressible and enforceable in a software program. This means we can’t put people in jail, prevent bribery, or monitor collusion. We also don’t get to mandate any agent’s behavior in the system—we can simply influence it indirectly through well-chosen incentives.
Our challenge is to choose the right incentives, rules, and interfaces such that agents in our system, whom we do not control, self-organize in a way that fulfills the purpose of our protocol.
Economic Mechanisms, Models, and Assumptions
To understand why cryptoeconomic design demands the rigorous simulation process that we will describe in part two, we must first review what mechanisms and models the traditional economic toolkit makes available to us and the key assumptions upon which they rest.
Mechanisms
A common concern of many cryptoeconomic protocols is the exchange of goods and services, as well as the allocation of resources. As is done in traditional economics, these questions may be resolved through market mechanisms.
For example, Bitcoin allocates a scarce resource—space for transactions within a block—using a first-price auction, a mechanism which has been in the context of internet applications for decades. In service protocols like The Graph, where market transactions take place off-chain, something like a negotiated market may be a more suitable mechanism, and we can draw on vast on algorithmic negotiation.
Not all behaviors neatly fit into a market paradigm. Nonetheless, behaviors can still be economically incentivized using other mechanisms, such as the inflationary block reward used to incentivize mining in blockchains like Bitcoin and Ethereum.
Behaviors also may be disincentivized. For example, proof of stake protocols do so directly by “” a bond submitted by a validator in response to the validator’s misbehavior, while proof of work protocols do so indirectly by imposing an opportunity cost on miners who don’t mine blocks on top of the correct chain.
Models
At the heart of most economic models dealing with human behavior lies the notion of expected utility. Utility is a numerical representation of how much an individual values a particular choice or outcome.
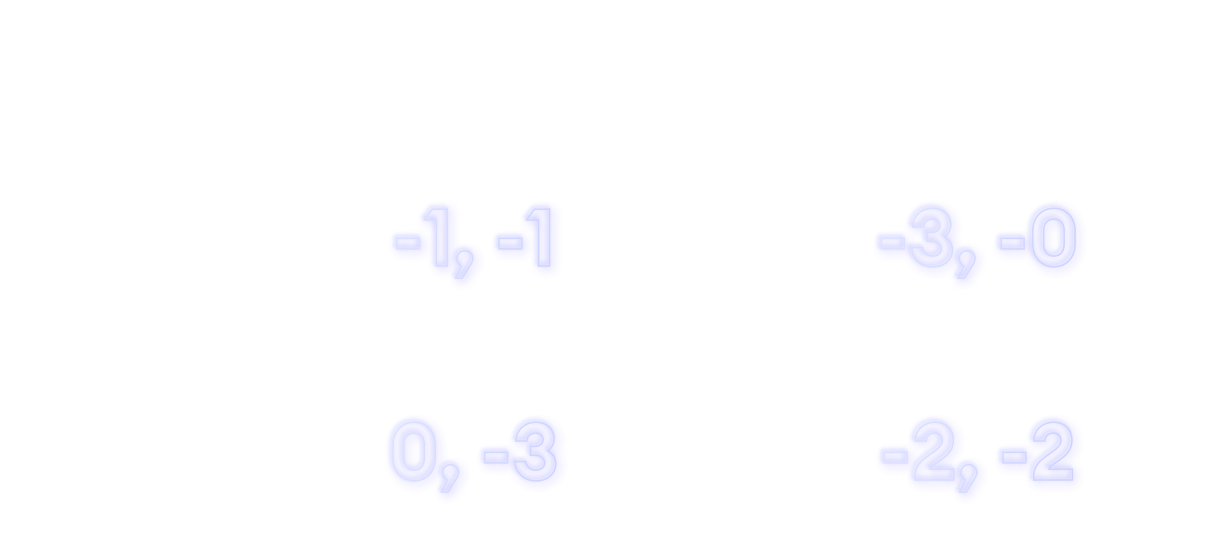
For example, consider a diagram like the one above, representing the prisoner’s dilemma game. The different cells in the matrix represent possible outcomes of the game and the utility of that outcome for each player respectively. In order to predict the strategies that players will deploy, game theory assumes that players attempt to maximize their expected utility.
Often, preferences for a given choice are modeled by a utility function, and it is assumed that individuals seek to maximize this utility subject to a set of constraints. In other words, we are solving a problem.
For instance, in consumer choice theory, a central question is what bundle of goods should a consumer choose, given a set of prices for those bundles and a budget.
A similar approach is also used in general equilibrium models of a market, which predict equilibrium outcomes based on the aggregate behavior of many individuals and firms who are all solving constrained optimization problems.
An important consequence of these models is that equilibria will be economically efficient, which is to say goods and services are allocated in a way that is optimal. This is quite a neat result, but one which must be interpreted judiciously.
These models imply that by leveraging market mechanisms, one needn’t know how to manually optimize the objective function defined as part of our system. We simply create the conditions by which the knowledge and actions distributed among the agents in our system lead to an efficient outcome. This provides a normative guide to how we might design a market that trends toward efficiency, but it doesn’t guarantee an accurate description for how our system will behave unless we are willing to take for granted numerous, often suspect, assumptions.
Assumptions and Limitations
There are many assumptions that are built into general equilibrium theory models of the economy, but here are just a few that bear mentioning:
- Full Rationality
Our market comprises rational, utility-maximizing participants. - Perfect Information
Agents in our system have perfect information. - No Nonlinearities
No monopolistic behavior or network effects exist.
There are many reasons to doubt the above assumptions. For example, countless experiments in the field of behavioral economics suggest we are not rational utility maximizers.
A simpler reason to mistrust the first two assumptions is that the human brain has finite computation and storage capacity. Furthermore, information isn’t perfectly distributed, but rather reaches us through social and technological networks. In other words, we make decisions with bounded rationality and partial information.
As for monopolistic behavior and network effects, examples of these are plentiful in the real world, and often go hand in hand. This is because industries with network effects tend to have winner-take-all dynamics. Also, in the cryptoeconomic setting, we don’t have the luxury of antitrust laws to prevent monopolies for the same reasons that we can’t prevent bribery or collusion.
So what are the consequences of rejecting the above assumptions?
The straightforward answer is that it undermines the specific models mentioned in the previous section. The not-so-obvious answer is more meta. Rejecting the above assumptions actually calls into question our ability to correctly model the aggregate behavior using any top-down statistical or closed-form analytical model.
This is because rejecting the above assumptions actually implies that economic systems are complex. To understand why that matters, let’s take a brief tour of complexity.
Complexity
Complexity describes systems that exhibit behaviors and properties that are not predicted by the constituent components. Or as :
“Many things have a plurality of parts and are not merely a complete aggregate but instead some kind of a whole beyond its parts.”

An image of the emergent patterns of a starling murmuration in flight. Or check out .
Take for example the awe-inspiring patterns formed by starlings in flight. It would be impossible to predict the emergent behaviors of the entire flock from examining a single starling. In complex systems, it’s the local interactions between all the interconnected components that lead to unexpected results.
The study of complexity has roots in general systems thinking, a movement pioneered by economist Kenneth Boulding and described in Gerald Weinberg’s seminal 1975 book, An Introduction to General Systems Thinking. In it, he describes how, in the absence of any simplifying assumptions, the computation required to model any system grows exponentially with respect to the number of constituent interrelated parts.
Consider the study of planetary motion. A high schooler can calculate the motion of a planet around the sun using pen and paper, while the lacks any closed-form solution.
To deal with these challenges, scientists have traditionally employed two classical techniques inspired by prior successes in the field of physics: Reducing the number of parts under consideration or using statistical analysis to only examine aggregate properties and behaviors of the system.
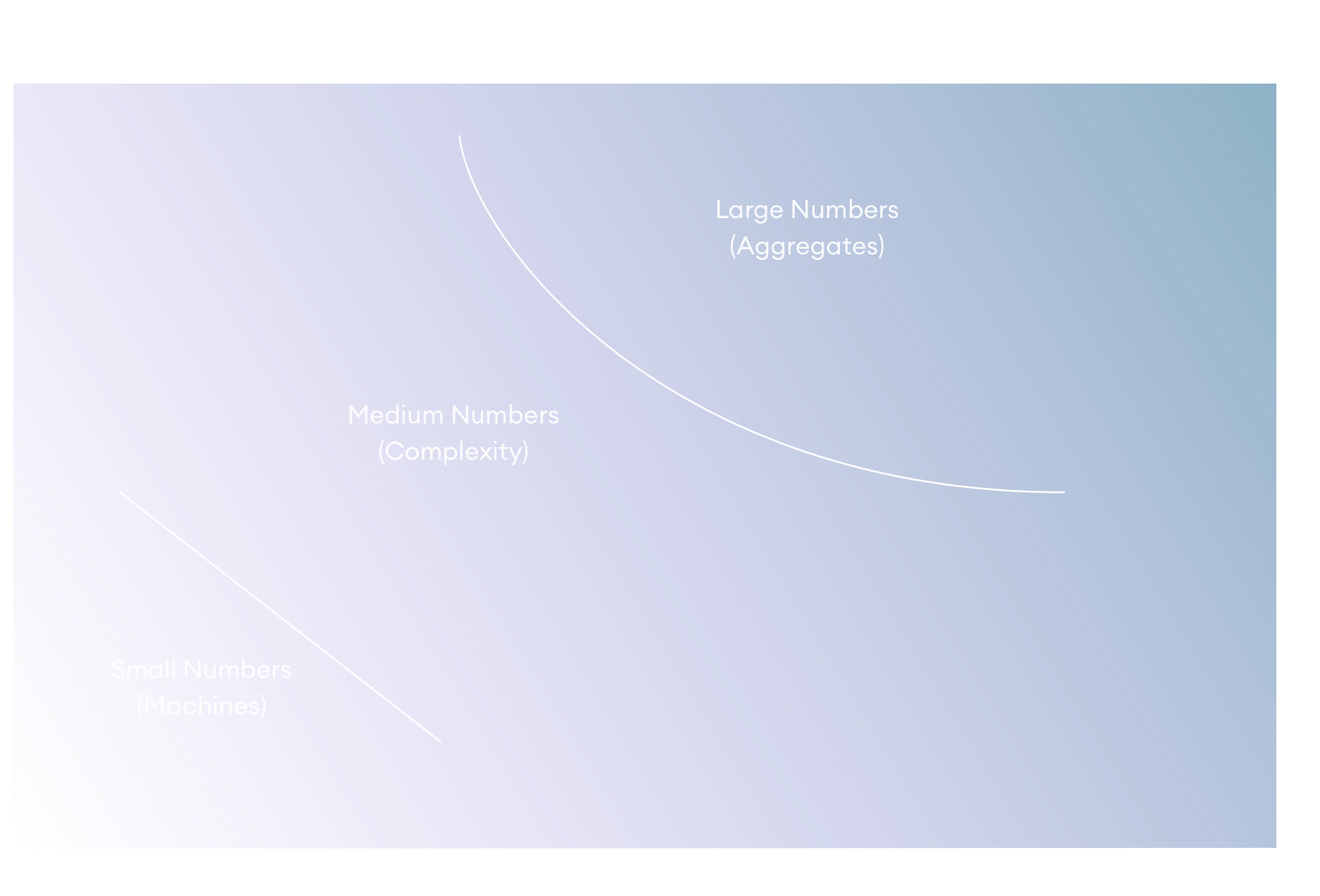
The reductionist approach works well when a part can be isolated from other parts and the influence of other parts can be safely ignored, such as we do when ignoring the gravitational pull of individual asteroids when computing the motion of the Earth around the sun.
The statistical approach works well when there are so many homogenous parts that the average behavior of a system is highly predictable, even if the behavior of individual parts is unknown. For example, consider the , which can relate properties like pressure and volume without accounting for the position and velocity of any individual atoms and molecules. These are systems in which the applies.
Most systems of interest to the social sciences, including economics, are medium number systems: Systems that have an irreducible number of interacting parts and whose parts are too heterogenous to support statistical analysis. Today, we would call these systems complex.
Complexity in Economics
In modeling systems, economists leverage both the reductionist and the statistical approach. For example, the prisoner’s dilemma game we showed earlier captures the individual actions of two players in a game. Such a setup permits a bottom-up analysis of the equilibrium behavior. However, computing an equilibrium in general is and as the number of players increases, games even exhibit .
Thus for modeling systems with many agents, economists have relied on the top-down statistical approach. Revisiting the assumptions from economics we covered earlier, we can see that one advantage of modeling humans as rational agents with perfect information is that it justifies the statistical approach by implying a high degree of homogeneity in the behaviors of agents in our system.
This mismatch of theory and reality, modeling a medium number system as one in which the law of large numbers applies, can have disastrous consequences. This is because it gives us a false sense of confidence that we have correctly modeled the system, leading to decisions that further exacerbate the effects of emergent phenomena.
For example, in the lead up to the 2007 subprime mortgage crisis, ratings agencies used flawed assumptions that ignored complexity in the housing market to assert that “80% of a collection of toxic subprime tranches were the ratings equivalent of U.S. Government bonds,” as Kyle Bass of Hayman Capital Advisors put it in his . Investors, driven by their belief in these models, took massive leveraged bets on subprime mortgages, leading to even more subprime mortgages being issued than had the models not existed in the first place.
The modern philosopher and mathematician Nassim Taleb popularized the term black swan to refer to such unforeseen events, in particular those whose effects are made stronger by nonlinearities. Nonlinearity describes systems where small variations of some input can lead to massive and disproportionate changes in some output. Nonlinearity is often associated with winner-take-all mechanics and network effects, which as discussed previously, are assumed to not be present by traditional economic models.
Another example of nonlinearity is in systemic risk or “too-big to fail,” as was also seen following the 2007 subprime mortgage crisis. Companies like American International Group (AIG) had to be bailed out because allowing them to fail would be disastrous to the system as a whole, whereas letting a company a tenth the size fail would have caused far less than a tenth of the damage.
In some respects, our task as cryptoeconomic designers is even more challenging than that of traditional economists. When the subprime mortgage crisis hit, central bankers were able to take extraordinary measures to put the economy on track, and legislators subsequently passed legislation intended to make sure it would never happen again. With cryptoeconomic protocols, a primary design goal is to make such extraordinary interventions impossible or extremely difficult. Otherwise, a small group of individuals would be able to undermine the system. This makes it all the more important that we predict and attempt to mitigate possible failure modes during our design phase.
Conclusion
So, where does this leave us? We have to acknowledge that the systems we are modeling are complex, and that this complexity poses inherent challenges to any top-down statistical model that ignores the inherent interconnectedness and heterogeneity of our system. A bottom-up approach that accounts for the dynamics of each individual part of the system would be far more preferable, but for most non-trivial cases, computing an exact bottom-up solution describing the behavior of our system is computationally intractable.
In , we’ll explore how we can borrow techniques from engineering and the social sciences, in particular dynamic systems models and agent-based models, to simulate how our system could behave using a bottom-up approach rather than trying to compute an exact solution. We’ll also explore how we plan to apply these tools for modeling and simulating The Graph.
